Factors of 72 | Pair Factors | Prime Factor | Factor Tree of 72

The factors of 72 are 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72. Factors of 72 are the numbers that divide the number 72 without leaving any remainder. Some numbers are known as pair factors of 72 since when we multiply these factors in pairs, it gives back the number 72. For example, 36 X 2 = 72. Also, these factors are both positive and negative. In this article, let us learn how to find factors of 72 along with solved examples. Scroll down to read more.

What Are the Factors of 72?

Factors of any number are the numbers that divide the number completely without leaving any remainder. If the given number is a prime number, then it doesn’t have more than one factor. Alternatively, if the given number is a composite number, then that particular number has more than one factor.

Since 72 is a composite number, it has multiple factors, and they are:

Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72 Negative Factors of 72: -1, -2, -3, -4, -6, -8, -9, -12, -18, -24, -36, and -72 Pair Factors of 72: (1, 72), (2, 36), (3, 24), (4, 18), (6, 12), and (8, 9) Prime Factors of 72: 2 × 2 × 2 × 3 × 3 = 23 × 32 Sum of Factors of 72: 195 Sum of Prime Factors of 72: 5

From the above, it is clear that 72 has 13 factors.

What are Factors of 72 in Pairs?

A pair of factors of 72 is a combination of two numbers that result in the numeral 72 after the multiplication of two numbers. They can either be a positive or negative pair. Here are the positive pairs and the negative pairs of 72.

Positive Pair Factors of 72

The positive pair factors of 72 are given below:

From the above table, (1, 72), (2, 36), (3, 24), (4, 18), (6, 12), and (8, 9) are the positive pair factors of 72.

Negative Pair Factors of 72

The negative pair factors of 72 are tabulated below:

From the above table, (-1, -72), (-2, -36), (-3, -24), (-4, -18), (-6, -12), and (-8, -9) are the negative pair factors of 72.

How To Find Factors of 72 by Division Method?

So, for the division method, you will divide all the numbers from 1 to 72 by 72. The numbers which leave a remainder are not factors of 72. Those numbers which don’t leave any remainder are the factors of 72.The numbers 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72 are factors of 72.

The following are the detailed steps for finding factors of 72 using the division method:

• 72 ÷ 1 = 72 (Remainder = 0)
• 72 ÷ 2 = 36 (Remainder = 0)
• 72 ÷ 3 = 24 (Remainder = 0)
• 72 ÷ 4 = 18 (Remainder = 0)
• 72 ÷ 6 = 12 (Remainder = 0)
• 72 ÷ 8 = 9 (Remainder = 0)
• 72 ÷ 9 = 8 (Remainder = 0)
• 72 ÷ 12 = 6 (Remainder = 0)
• 72 ÷ 18 = 4 (Remainder = 0)
• 72 ÷ 24 = 3 (Remainder = 0)
• 72 ÷ 36 = 2 (Remainder = 0)
• 72 ÷ 72 = 1 (Remainder = 0)

Since the number 72 is a big number, the division method is a lengthy method to find factors of 72.

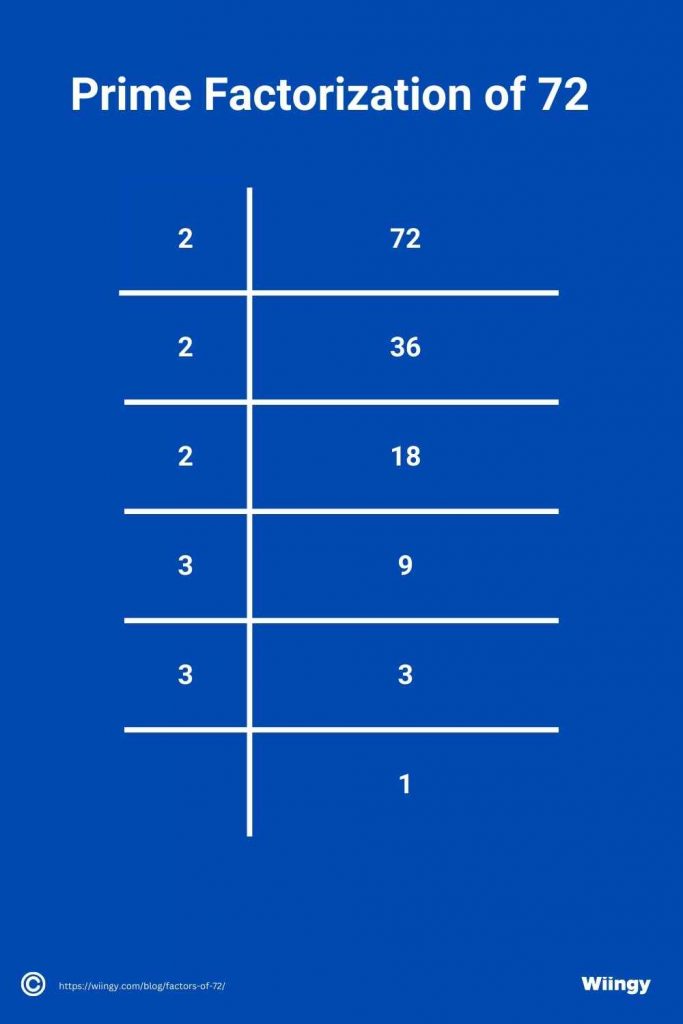
What Are 72 Prime Factors?

Since 72 is a composite number, let’s find the prime factorization of 72.

• Step 1: Firstly, 72 with the smallest prime number that is divisible by 72. Hence, the smallest prime number that is divisible by 72 is 2.
  72 ÷ 2 = 36
• Step 2: Now divide the number 36 (quotient) with the least prime number, which is 2.
  36 ÷ 2 = 18
• Step 3: Now divide the number 18, with least prime number which is again 2.
  18 ÷ 2 = 9
• Step 4: Now divide the number 9 with the least prime number 9 is divisable by. Since the number 9 is not divisible by 2, we will use the next smallest prime number which is 3 because 3 can divide 9.
  9 ÷ 3 = 3
• Step 5: Divide the number 3 (quotient) by 3 because it can only be divided by 3 as it’s a prime number.
  3 ÷ 3 = 1

So, in conclusion, we can see that 2³ × 3² or 2 x 2 x 2 x 3 x 3 is the prime factorization of 72. It means that 2 and 3 are the prime factors of 72.

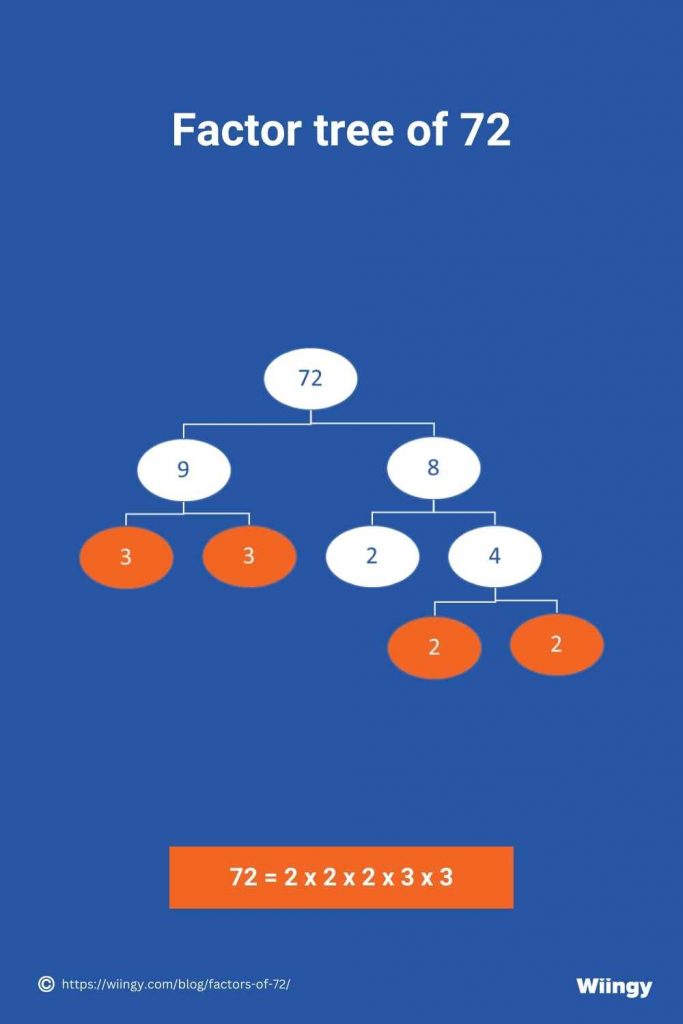
What Is the Factor Tree for 72?

Students can also use the factor tree to find the prime factors of 72. In a factor tree, we divide a number until the answer becomes 1, and the factors are written in the form of branches of a tree. Then, the last factors are circled, and they are the prime factors of the number. The detailed steps on how to do this are explained below:

• Step 1: Let’s place the number 72 at the top of the factor tree and write down 72 in pairs, that is, 9 and 8.
• Step 2: As both 8 and 9 are composite numbers, we have to divide the factors of 8 and 9 as branches until they become prime numbers. We will now divide 9 into 3 and 3.
• Step 3: Whereas for the number 8, the factors that we can divide it with are 4 and 2, indicating that we need to divide the factors of a number until they become prime numbers.
• Step 4: As we can see, 2 is a prime number but 4 is not, so we will split 4 into 2 and 2.
• Step 5: As 2 is a prime number, we cannot divide it. Now we will see all the prime numbers in the factor tree as the branches.

Circling all the branches 2 x 2 x 2 x 3 x 3 = 72, which are prime factors of 72. There are many ways on which we can write the factor tree of 72.

Below is an image representation of the factor tree of 72.

Solved Examples on Factors of 72

Here are some solved examples that include common questions and answers to make your concepts clearer.

What are the factors of 72 that add up to 17?
To find the factors of 72 that add up to 17, we need to list out all the factors.
The factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72. After adding them in combinations, you can find the factors that make 17 and they are:
8 + 9 = 17
9 + 8 = 17
So, 8 and 9 are the factors of 72 that add up to 17.

What are the factors of 72 and 32?
The factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72.
The factors of 32 are 1, 2, 4, 8, 16, and 32.
Hence, from the above, the common factors of 72 and 32 is 1, 2, 4, and 8.
The highest common factor between 72 and 32 is 8.

What are three common factors of 24 and 72?
The factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24.
The factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72.
Hence, from the above, the common factors of 24 and 72 is 2, 3, and 4.
The highest common factor between 24 and 72 is 12.

What is the sum of all the factors of 72?
To find the sum of all the factors of 72, we need to add all the factors of 72.
Adding 1 + 2 + 3 + 4 + 6 + 8 + 9 + 12 + 18 + 24 + 36 + 72 = 195.
Hence the sum of all the factors of 72 are 195.

How are the factors of 36 related to 72?
The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36.
Factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72.
Hence, from the above, the common factors of 36 and 72 is 1, 2, 3, 4, 6, 9, 12, 18 and 36.
The highest common factor between 36 and 72 is 36.

What are the common factors of 54 and 72?
The factors of 54 are 1, 2, 3, 6, 9, 18, and 54.
The factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72.
Hence, from the above, the common factors of 54 and 72 is 1, 2, 3, 6, 9, and 18.
The highest common factor between 54 and 72 is 18.

FAQs on Factors of 72

List all the factors of 72
1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72 are the 72 factors.

What are the factors of -72?
-1, -2, -3, -4, -6, -8, -9, -12, -18, -24, -36, and -72 are the factors of -72.

What are the composite factors of 72?
Composite numbers are the ones that are described as whole digits and have three or more whole number factors.
4, 6, 8, 9, 12, 18, 24, 36 and 72 are the composite factors of 72.

What are the prime factors of 72?
2 x 2 x 2 x 3 x 3 = 2³ × 3² are prime factors of 72.

What are the common factors of 72?
1 and 3 are the common factors of 72.

What are the pair factors of 72?
(1, 72), (2, 36), (3, 24), (4, 18), (6, 12), and (8, 9) are pair factors of 72.

What are the positive factors of 72?
1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72 are positive factors of 72.

We hope that this article on factors of 72 has been helpful to you and that you can quickly find the factors of 72 and even employ all of the methods. Feel free to leave a comment below if you have any questions or concerns. We will look into it and provide you with a response as soon as possible.