What Are the Factors of 25? | Prime Factorization and Factor Tree of 25

The factors of 25 can be defined as the list of integers that can be split evenly into 25. In other words, those numbers that are completely divisible by 25 without leaving any remainder are called the factors of 25. In this article we will discuss the factors of 25, the prime factorization and factor tree of 25, along with some solved examples and FAQs on factors of 25.

What Are the Factors of 25?

The factors of 25 can be defined as the numbers which are completely divisible by the number 25, or you can define it as two numbers when multiplied by each other, giving the result of 25. The factors of 25 can be listed as 1, 5, and 25. The prime factor of 25 is 5 X 5=25. The factor of 25 has two-factor pairs, one positive, (1, 5, and 25), and the other one is a negative pair, (-1, -5, and -25).

25 Factors: 1, 5, and 25 Positive Factors of 25: 1, 5, 25 Negative Factors of 25: -1, -5 and -25 Pair Factors of 25: (1, 25), (5,5) Sum of Factors of 25: 31 Prime Factors of 25: 5 Sum of Prime Factors of 25: 5

How To Find Factors of 25?

Factors of 25 are a list of whole numbers that can be divided by 25 into equal parts and not leave any remainder. As a result, the factors of 25 cannot be decimal or fractional numbers. All the factors of 25 can be calculated using either the multiplication or the repeated addition method. The steps to calculate the factors of 25 using both methods are given below.

How To Find Factors of 25 using Multiplication Method?

The steps to find factors of 25 using multiplication method are given below:

• Step 1: We can calculate the factors of 25 using the multiplication method. For this method, we check what pairs of numbers can be multiplied with each other in order to get the result of 25. So, for this, we need to multiply the number 25 by a series of natural numbers, from 1 to 9. The numbers that get completely divided by 25, without leaving any remainder, are the factors of 25.
• Step 2: We know that the multiples of 25 are those numbers that are completely divisible by 25. Now, let’s create a list of those numbers and their pairs. For example, 1 X 24 = 25, so (1, 25) is the first pair, and 5 X 5 = 25, so (5, 5) is the second pair, and as 5 is a prime number, it cannot be split any further.

So, the factors of 25 are 1, 5, and 25.

How To Find Factors of 25 using Division Method?

The steps to find factors of 25 using the division method are given below:

• Step 1: A number is a factor of itself, and 1 is the factor of all natural numbers. So, 1 and 25 are factors of 25.
• Step 2: Now let’s divide 25 with a series of whole numbers starting from 1 to 9, and the division of the number which leaves 0 as the remainder is the multiples of 25. The table is given below:

Factors of 25 using Division Method

25 ÷ 1= 25 25 ÷ 2= 12.5 (not divisible by 25 completely) 25 ÷ 3= 8.3 (not divisible by 25 completely) 25 ÷ 4= 6.2 (not divisible by 25 completely) 25 ÷ 5= 5 25 ÷ 6= 4.1 (not divisible by 25 completely) 25 ÷ 7= 3.5 (not divisible by 25 completely) 25 ÷ 8= 3.1 (not divisible by 25 completely) 25 ÷ 9= 2.7 (not divisible by 25 completely)

Hence, the factors of 25 are 1, 5, and 25.

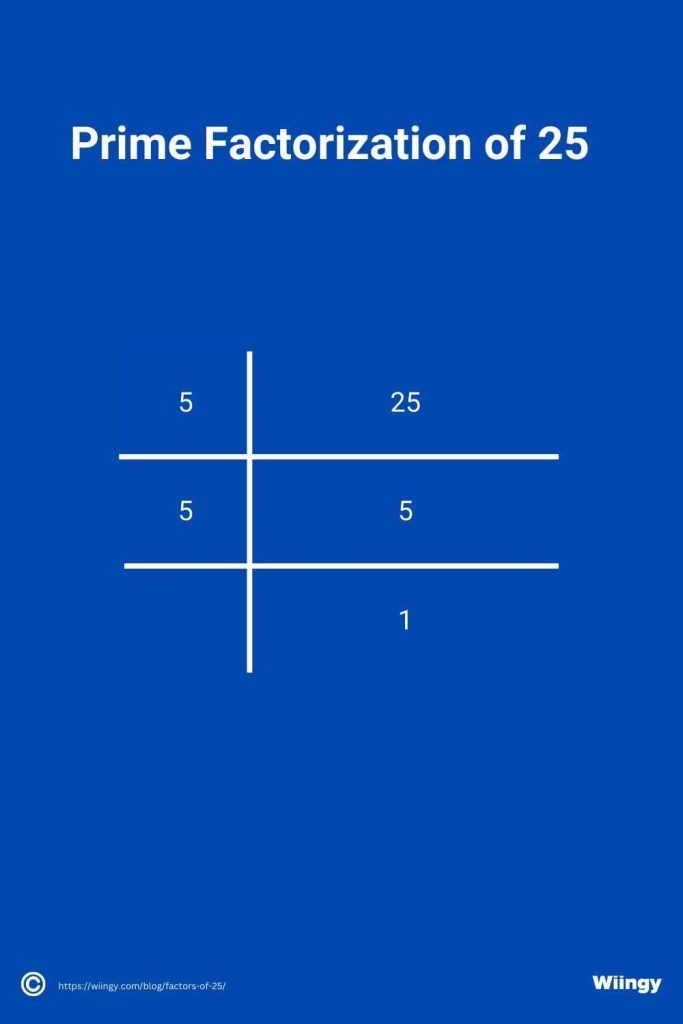
Calculating the Prime Factors of 25 by Prime Factorization

Prime factorization can be defined as expressing a composite number as the product of its prime factors. Now, to find the prime factorization of 25, we need to divide it by its smallest prime factor that is divisible by 25.

• The smallest prime number that is divisble by 25 is 5. 
• 25  ÷ 5 = 5. 
• Now, let’s divide 5 by its smallest prime factor and let’s continue till we get 1 as the quotient.
• When we divide the number 25 with 25, we will get 5 as the quotient.
• Now dividing the number 5 with smallest prime number that is divisible by 5 is 5.
• Hence the quoitent here is 1.
• Hence the prime factors of 25 is 5.

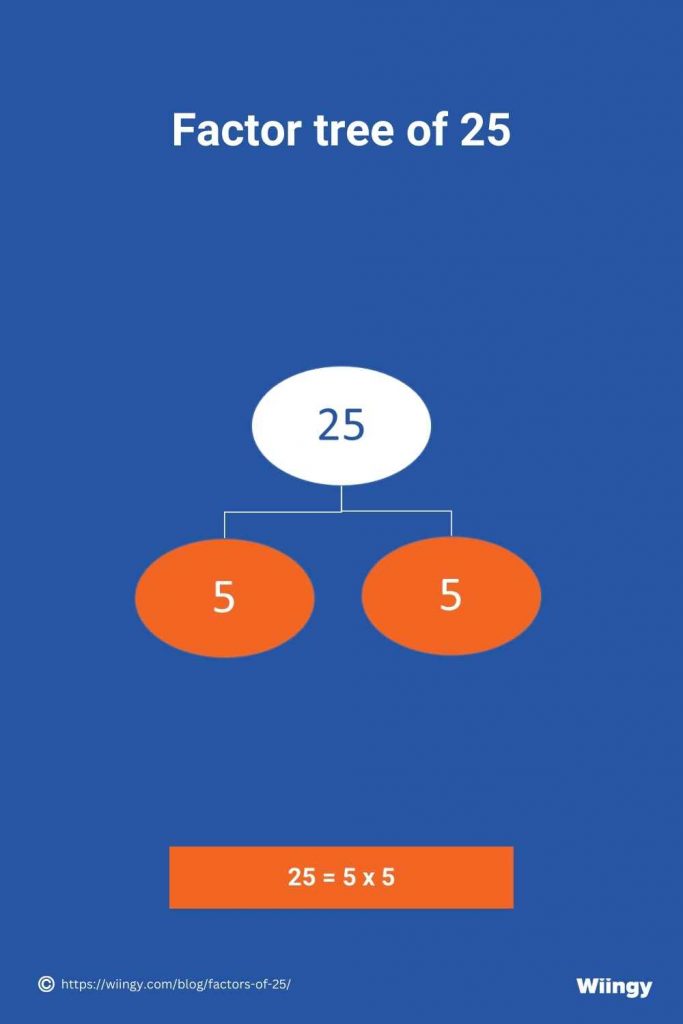
Factor Tree of 25

The steps to find factor tree of 25 has been explained below:

• Step 1: Place the number 25 at the top of the factor tree.
• Step 2: Now write the pair factor of 25, which when multiplied by the number 25 gives the answer. Here we are choosing 5,5 as the pair factor.
• Step 3: Because 5 is a prime number, it cannot be divided further. 

Hence the prime factors of 25 from the factor tree is 5.

Solved Examples on Factors of 25

Q 1: What are the factors of 25?
A 1: 1, 5, and 25 are the factors of 25 as these numbers are completely divisible by 25.

Q 2: Find the common factors of 24 and 25.
A 2: The factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24.
The factors of 25 are 1, 5, and 25.
Therefore, the common factor of 24 and 25 is 1.

Q 3: What is the sum of all the factors of 25?
A 3: The factors of 25 are 1, 5, and 25.
The sum of factors of 25 can be calculated as 1 + 5 + 25= 30.
therefore, the sum of all the factors of 25 is 30.

Q 4: What are the factors of 25 in pairs?
A 4: There are two factor pairs of 25, one positive and one negative.
Positive pair- (1, 5, 25).
Negative pair- (-1, -5, and -25).

Q 5: Find the common factors of of 25 and 30.
A 5: The factors of 25 are 1, 5, and 25.
The factors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30.
Therefore, the common factors of 25 and 30 are 1, and 5.

FAQs on Factors of 25

Find the prime factors of 25.
To find the prime factor of 25, we need to divide it by its smallest prime factor, i.e., 5.
25 ÷ 5= 5
Now, let’s divide 5 by its smallest prime factor and let’s continue till we get 1 as the quotient. Since 5 is a prime number it cannot be split further.
Hence, 5 is the prime factor of 25.

What are the common factors of 25 and 75?
The factors of 25 are 1, 5, and 25.
The factors of 75 are 1, 3, 5, 15, 25, and 75.
The common factors of 30 and 75 are 1, 5, and 25.

What are the factors and prime factors of 25?
The factors of 25 are 1, 5, and 25 as these numbers are completely divisible by 25.
The prime factor of 25 is 5 as 5 is a prime number and cannot be split further.

Find the common factors of 30 and 36.
The factors of 25 are 1, 5, and 25.
The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36.
Therefore the common factors of 30 and 36 is 1.

Find the common factors of 30 and 100.
The factors of 25 are 1, 5, and 25.
The factors of 100 are 1, 2, 4, 5, 10, 20, 25, 50, and 100.
Therefore, the common factors of 30 and 100 are 1, 5, and 25.

We hope this article on factors of 25 is helpful to you. If you have any questions related to this page, ping us through the comment section below and we will get back to you as soon as possible.