Factors of 14 | Prime Factorization of 14 | Factor Tree of 14

The factors of the given number 14 are the numbers that can divide 14 with zero remainders. The pair factors can be written in either positive or negative form. In this article, you will learn about factors of 14 using the prime factorization method, factor tree method, and division method.

What Are the Factors of 14?

The factors of 14 are the numbers that can divide that number completely without leaving behind any remainder. For every number, there are both positive and negative factors. Based on the count of the factors of a number, it can be classified as a prime number or composite number. A prime number is a number for which there are only two or less than two numbers as factors while a composite number has more than two numbers as its factors. Thus, 14 is a composite number, as it has more than two numbers as factors and those numbers are 1, 2, 7, and 14.

Factors of 14: 1, 2, 7, and 14.

Negative Factors of 14: -1, -2, -7, and -14.

Prime Factorization of 14: 2 x 7

Pair Factors of 14: (1, 14) and (2, 7)

Prime Factors of 14: 2, and 7

Sum of Factors of 14: 24

Sum of Prime Factors of 14: 9

What Are the Factors of 14 in Pairs?

The pair factors of a number can be both positive and negative. The combination of two numbers which on multiplying together gives 14 are the pair factors of 14.

Positive Pair Factors of 14

The positive pair factors of 14 are (1, 14) and (2, 7).

Negative Pair Factors of 14

The negative pair factors of 14 are (-1, -14) and (-2, -7).

What Is the Prime Factorization of 14?

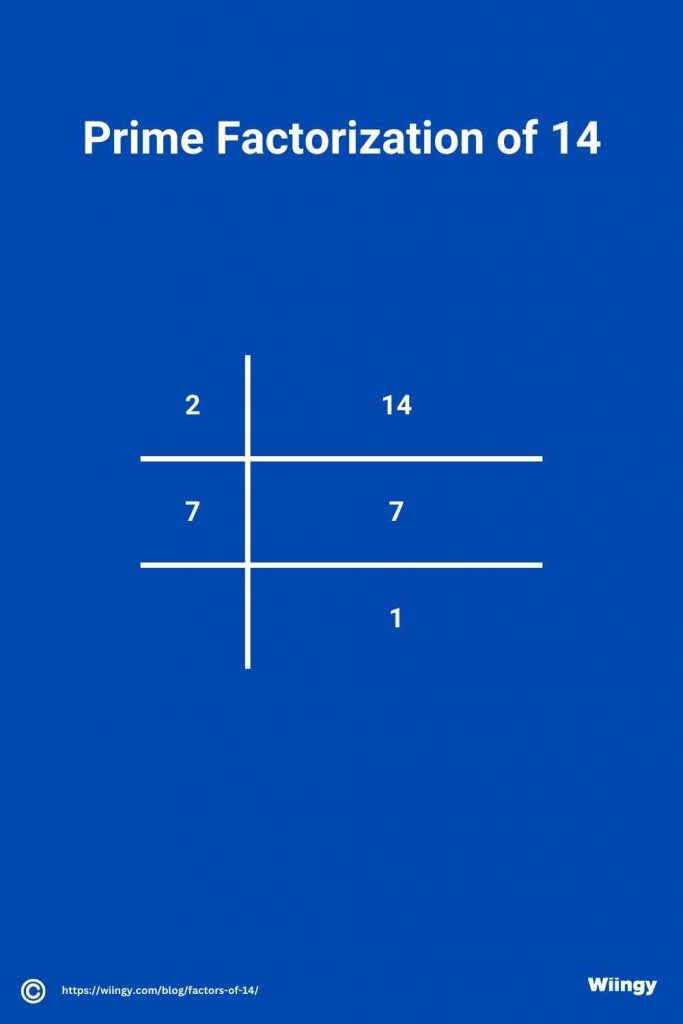
Prime factorization is a method used to identify the prime factors of 14. The following are the steps involved in that process:

• Step 1: Let’s place the number 14 at the top and let’s divide it by the smallest number which is two.
• Step 2:  We get 7 as the quotient. As 7 is a prime number, it’s only divisible by itself. That is, 7 ÷ 7 = 1
• Step 3: Now the remaining quotient is 1 and so we can’t divide it further. So, the prime factors of 14 are 7 and 2.

Its further well represented through the image given below:

What Is the Factor Tree of 14?

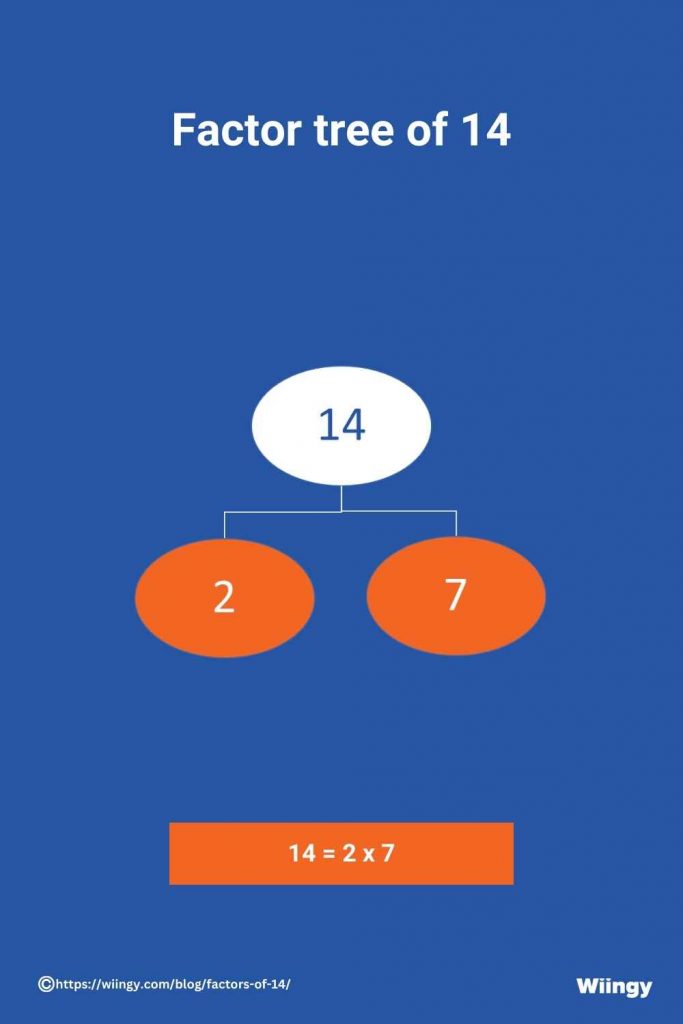
The prime factors of 14 can be found using the factor tree method. For this place 14 at the top of the factor tree. Then split the numbers into their factors and then write the set of the pair factors on its branches. And this process should be continued till the factors turn into prime numbers. And so finally by identifying all the prime numbers we will get all the prime factors of 14. The steps involved in this process are given below:

• Step 1: Let’s place the number 14 at the top and write down 14 in pairs, that is, 7, 2.
• Step 2: The branches in the factor tree will now be all the prime numbers. Circling all the branches, 2 x 7 which are the prime factors of 14.

There are many ways in which we can write the factor tree of 14. Below is an image representation of the factor tree of 14, choosing 2 and 7 as pair factors of 14.

How to Find Factors of 14 Through Division Method?

Any numbers that divide 14 without leaving any remainder are known as factors of 14. Through the division method, we can find the factors of 14 by a dividing sequence of numbers. The steps are mentioned below for your clear understanding.

• 14 ÷ 1 = 14
• 14 ÷ 2 = 7
• 14 ÷ 7 = 2

Therefore, the factors of 14 are 1, 2, 7, and 14.

Solved Examples of 14 Are as Follows:

What are the factors of 14?
The factors of 14 are 1, 2, 7, and 14.

What are the pair factors of 14?
The pair factors of 14 are (1, 14) and (2, 7)

What is the sum of the factors of 14?
The sum of the factors of 14 is 24.

What is the sum of the prime factors of 14?
The sum of the prime factors of 14 is 9.

Frequently Asked Questions

What are the multiples of 14?
The multiples of 14 are 14, 28, 42, 56, 70, 84, 98, 112, 126, 140, 154, 168, 182, 196, 210, 224, 238, 252, 266, 280, 294, 308, 322, 336, 350, etc.

What are the factors of 2 and 14?
The factors of 2 and 14 are 1, 2 and 1, 2, 7, and 14.

How do you divide 14?
The number 14 is divisible by the numbers such as 1, 2, 7, and 14.

What are the factors of 14?
The factors of 14 are 1, 2, 7, and 14.

Is 14 divisible by 4?
No, the number 14 is not completely divisible by the number 4.