Find top 1-on-1 online tutors for Coding, Math, Science, AP and 50+ subjects

Table of Contents

AP

Central Limit Theorem Explained!

A statistical theory called the central limit theorem states that when a large sample size has a small variance, samples will be normally distributed and their means will be about equal to those of the total population.

The central limit theorem permits one to assume that the sampling distribution of the mean would often be normally distributed hence, it is helpful for examining big data sets. This makes statistical analysis and inference simpler.

A particular random variable of importance in many real-time applications is the sum of several independent random variables. We may utilize the CLT in these circumstances to support the adoption of the normal distribution.

Want to learn AP Statistics from experts? Explore Wiingy’s Online AP Statistics tutoring services to learn from top mathematicians and experts.

What is central limit theorem?

If the sample size is high enough, the central limit theorem states that the sampling distribution of the mean will always be normally distributed. No matter if the population has a distribution or not, the mean’s sample distribution will be normal.

In simpler terms, the theorem states that the distribution of the sample means will be normally distributed regardless of the underlying distribution of population given that the sample size is large enough typically greater than thirty.

Assumptions of the central limit theorem

  • The sample size should be large enough because the larger the sample size more likely it will be representative of the population set.
  • The samples drawn should be random and should follow the condition of randomization.
  • The drawn samples should not influence one another i.e., the samples need to be independent of each other.
  • The sample size should not be greater than ten percent of the total population when the sampling is done without replacement.

Implications of the central limit theorem

From the theorem, we can conclude the following facts.

  • The sample mean is an unbiased estimator of the population mean

It implies,

Let {{X}_{1}},{{X}_{2}},{{X}_{3}}....,{{X}_{n}} be a random sample from population which has a mean \mu and variance {{\sigma }^{2}}.

Then:

\\overline{x}\,=\frac{1}{n}\sum\limits_{i=1}^{n}{{{X}_{i}}}

is an unbiased estimator of\mu.

  • The sample standard deviation can be used as an estimator of the population standard deviation

As the central limit theorem is used for populations greater than 30 the difference between the calculated sample standard deviation and the population standard deviation becomes very negligible.

The ratio of the sample standard deviation and the population standard deviation is:

    \[\frac{{{s}_{p}}}{{{s}_{s}}}=\sqrt{1-\frac{1}{n}}\approx 1-\frac{1}{2n}\]

And for large populations\frac{1}{2n} becomes negligibly small.

  • The sample mean follows a normal distribution, which allows us to use the normal distribution for inferential statistics

If there are not too many extreme values in the distribution, the sum (and hence the mean) of any set of random variables tends asymptotically to a normal distribution and hence we can use the statistical formulas we use for normal distribution.

ap statistics practice tests and past papers download

Applications of the central limit theorem

  • Election polls feature among the most often used CLT applications. to determine the confidence intervals used in news reports to represent the percentage of people who support a candidate.
  • If the distribution is unknown or not normal, we assume that the sample distribution complies with CLT’s definition of normality. Due to the method’s assumption that the population is distributed regularly. This facilitates data analysis techniques like building confidence intervals.
  • It is also used to measure the mean or average family income of a family in a particular region.
  • The central limit theorem is frequently used by economists when analyzing sample data to make generalizations about a population.
  • The central limit theorem is frequently used by manufacturing facilities to determine how many of their goods are faulty.
  • By taking more samples from the population, we can more precisely estimate the population mean while also reducing the sample means deviation.
  • We may utilize the sample mean to produce a range of values that is likely to include the population mean.

Central limit theorem formula

The formula for sample means:

    \[Z=\frac{\overline{x}\,-\mu }{\frac{\sigma }{\sqrt{n}}}\]

The proof for the formula:

Considering {{x}_{1}},{{x}_{2}},{{x}_{3}}....,{{x}_{n}}which are independent and have a mean \mu and a finite variance {{\sigma }^{2}},then taking a random variable {{Z}_{n}}

We get

 

    \[{{Z}_{n}}=\frac{\overline{{x}_{n}}\,-\mu }{\frac{\sigma }{\sqrt{n}}}\]

The other formulas used are

{{\mu }_{\overline{x}\,}}=\mu and {{\sigma }_{\overline{x}\,}}=\frac{\sigma }{\sqrt{n}}.

Where,

{{\mu }_{\overline{x}\,}}=sample mean

\mu=population mean

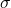{{\sigma }_{\overline{x}\,}}=sample standard deviation

\sigma=population standard deviation

n=sample size

Steps to solve a problem using the central limit theorem

  • Use the formula to find the z-score
  • The z-table is referred to find the ‘z’ value obtained
  • Central theorem including “>”:  the z-score needs to be subtracted from 0.5
  • Central theorem including “<”: 0.5 needs to be added to the z-score 
  • Central theorem including “between”: the formula is used.
  • The z-value is calculated along with the x bar.

Visualizing the central limit theorem

  • Using histograms to demonstrate the normal distribution of sample means

When we have to usually represent the sample means it would be a continuous curve because it is a continuous probability distribution where the values lie in a symmetrical fashion mostly situated around the mean.

But with the central limit theorem, we can figure the frequency of the occurrence of the values because the means of each value is calculated and hence represent a given data as a histogram.

Solved examples

Example 1: The data of heights of the male population follows a normal distribution. Its mean and standard deviation are 70 inches and 15 inches, respectively. If we consider the records of 45 males, then calculate the standard deviation of the selected sample?

Solution 1:

 Mean of the population \mu =70

Standard deviation of the population = 15

sample size n = 45

Standard deviation is given by:

    \[{{\sigma }_{\overline{x}\,}}=\frac{\sigma }{\sqrt{n}}\]

    \[<span class="ql-right-eqno"> (1) </span><span class="ql-left-eqno"> </span><img src="https://wiingy.com/assets/wp-content/ql-cache/quicklatex.com-fbcfd0bbb9739c5f127874a8fd58ef91_l3.png" height="161" width="583" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{align*} <!-- /wp:paragraph --> <!-- wp:paragraph --> & {{\sigma }_{\overline{x}\,}}=\frac{15}{\sqrt{45}} \\ <!-- /wp:paragraph --> <!-- wp:paragraph --> & {{\sigma }_{\overline{x}\,}}=\frac{15}{3\sqrt{5}} \\ <!-- /wp:paragraph --> <!-- wp:paragraph --> & {{\sigma }_{\overline{x}\,}}=\frac{5}{\sqrt{5}}=\sqrt{5} \\ <!-- /wp:paragraph --> <!-- wp:paragraph --> \end{align*}" title="Rendered by QuickLaTeX.com"/>\]

Hence the standard deviation would be 2.236

Example 2: A set of samples has been collected from a larger sample and the sample mean values are 34.6,67,90,12.8,45.2. Find the population mean.

Solution 2:

The population mean values can be calculated using the formula {{\mu }_{\overline{x}\,}}=\mu

Which implies,

 

    \[<span class="ql-right-eqno"> (2) </span><span class="ql-left-eqno"> </span><img src="https://wiingy.com/assets/wp-content/ql-cache/quicklatex.com-8b350d666db39f4e7ef15043d3db85f6_l3.png" height="133" width="727" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{align*} <!-- /wp:paragraph --> <!-- wp:paragraph --> & {{\mu }_{\overline{x}\,}}=\frac{34.6+67+90+12.8+45.2}{5} \\ <!-- /wp:paragraph --> <!-- wp:paragraph --> & {{\mu }_{\overline{x}\,}}=\frac{249.6}{5} \\ <!-- /wp:paragraph --> <!-- wp:paragraph --> & {{\mu }_{\overline{x}\,}}=49.92 \\ <!-- /wp:paragraph --> <!-- wp:paragraph --> \end{align*}" title="Rendered by QuickLaTeX.com"/>\]

Hence the population mean is 49.92

Example 3: The mean age of people living in a city is 40 years and the standard deviation is 9 years. What is the variance and mean for sample sizes 81 and 9.

Solution:

The variance can be calculated by taking the squaring the standard deviation.

{{\sigma }_{\overline{x}\,}}=\frac{\sigma }{\sqrt{n}}is the standard deviation formula.

For the sample size 81,

    \[<span class="ql-right-eqno"> (3) </span><span class="ql-left-eqno"> </span><img src="https://wiingy.com/assets/wp-content/ql-cache/quicklatex.com-b63c8546bdfc3868532f58aafbb0433f_l3.png" height="136" width="552" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{align*} <!-- /wp:paragraph --> <!-- wp:paragraph --> & {{\sigma }_{\overline{x}\,}}=\frac{9}{\sqrt{81}} \\ <!-- /wp:paragraph --> <!-- wp:paragraph --> & {{\sigma }_{\overline{x}\,}}=\frac{9}{9}=1 \\ <!-- /wp:paragraph --> <!-- wp:paragraph --> & \\ <!-- /wp:paragraph --> <!-- wp:paragraph --> \end{align*}" title="Rendered by QuickLaTeX.com"/>\]

Hence the variance is 1 and the mean is 40.

For the sample size 9 the central limit theorem cannot be applied as the size needs to be greater than 30.

Example 4: A distribution has a mean of 60 and a standard deviation of 24. If 121 samples are randomly drawn from this population then using the central limit theorem find the value that is five sample deviations above the expected value.

Solution 4:

We know that the mean of the sample equals the mean of the population according to the theorem.

Hence, mean = 60.

Standard deviation formula {{\sigma }_{\overline{x}\,}}=\frac{\sigma }{\sqrt{n}}

Substituting the values

    \[<span class="ql-right-eqno"> (4) </span><span class="ql-left-eqno"> </span><img src="https://wiingy.com/assets/wp-content/ql-cache/quicklatex.com-d31d8e2f9afd5774eb022b7b73264c40_l3.png" height="109" width="585" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{align*} <!-- /wp:paragraph --> <!-- wp:paragraph --> & {{\sigma }_{\overline{x}\,}}=\frac{24}{\sqrt{121}} \\ <!-- /wp:paragraph --> <!-- wp:paragraph --> & {{\sigma }_{\overline{x}\,}}=\frac{24}{11}=2.18 \\ <!-- /wp:paragraph --> <!-- wp:paragraph --> \end{align*}" title="Rendered by QuickLaTeX.com"/>\]

Hence the value that is five sample deviations above is

    \[<span class="ql-right-eqno"> (5) </span><span class="ql-left-eqno"> </span><img src="https://wiingy.com/assets/wp-content/ql-cache/quicklatex.com-e7923790bcf100d2708d5818ae47ad1a_l3.png" height="99" width="557" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{align*} <!-- /wp:paragraph --> <!-- wp:paragraph --> & 60+5(2.18) \\ <!-- /wp:paragraph --> <!-- wp:paragraph --> & =60+10.9 \\ <!-- /wp:paragraph --> <!-- wp:paragraph --> & =70.9 \\ <!-- /wp:paragraph --> <!-- wp:paragraph --> \end{align*}" title="Rendered by QuickLaTeX.com"/>\]

Example 5: The average weight of a can is 50 pounds which have a standard deviation of 20 pounds. Taking a sample of 50 cans that are selected at random and then their weights are calculated, what is the probability that the mean weight of the sample is less than 30 pounds?

Solution 5:

Population mean: \mu =50 pounds

Population standard deviation: \sigma =40pounds

Sample size: n=50

Now we use , z-score, and we get,

The sample standard deviation:

    \[{{\sigma }_{\overline{x}\,}}=\frac{\sigma }{\sqrt{n}}\]

And,

    \[{{\sigma }_{\overline{x}\,}}=\frac{40}{\sqrt{50}}\]

  = 5.66

Finding the  z- score for the value of x=30 pounds

    \[{{Z}_{n}}=\frac{\overline{{x}_{n}}\,-\mu }{\frac{\sigma }{\sqrt{n}}}\]

    \[{{Z}_{n}}=\frac{30-50}{5.66}=\frac{-20}{5.66}=-3.53\]

Using z- score table OR normal cdf function on a statistical calculator,P(z<-3.53)=0.00020778

    \[0.00020778\times 100=0.0207\]

Hence, the probability that the weight of the can is less than 40 pounds is 0.0207%

Conclusion

The central limit theorem is very widely used because it states that if we have sufficiently large samples from the population the distribution of samples can be normally distributed, and all the statistical calculations can be made for a data set with very large populations. Because of how the theorem helps to come to mathematical conclusions about huge sets of data, it is used in a lot of real-life situations and conditions. We have also seen how it helps in visualizing data which helps with the analysis and interpretation of the said data.

Want to learn AP Statistics from experts? Explore Wiingy’s Online AP Statistics tutoring services to learn from top mathematicians and experts.

Frequently asked questions (FAQs)

What is sampling distribution?

A sampling distribution refers to a probability distribution of a statistic that comes from choosing random samples of a given population. 

What is the z-score?

Z-score is a statistical measurement that describes a value’s relationship to the mean of a group of values. Z-score is measured in terms of standard deviations from the mean.

What is randomization?

In the statistical theory of the design of experiments, randomization involves randomly allocating the sample space across the population.

What is standard deviation?

Standard Deviation is a measure that shows how much variation or how dispersion from the mean exists. 

What is the normal distribution?

Normal distribution, also known as the Gaussian distribution, is a probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean.

References

Kwak, S. G., & Kim, J. H. (2017). Central limit theorem: the cornerstone of modern statistics. Korean journal of anesthesiology, 70(2), 144-156.

Rosenblatt, M. (1956). A central limit theorem and a strong mixing condition. Proceedings of the national Academy of Sciences, 42(1), 43-47.

Get 1-on-1 online AP Statistics tutor