AP Statistics

What is Normal Distribution?

Q: How many measures of variability are there?

There are four measures of variability which are variance, standard deviation, interquartile range, and range.

Q: What is the t-distribution?

Existing intelligence Compared to the conventional normal distribution; the t-distribution increases the chance of observations in the distribution's tails.

Q: What are the two types of the probability distribution?

Discrete and continuous probability distributions are the two main categories in which probability distributions fall. There are several varieties of probability distributions within each category. standard deviation.

Q: What is the standard deviation?

A "typical" variation from the mean is shown by the standard deviation. Because it uses the data set's original units of measurement, it is a well-liked measure of variability.

Q: What is a histogram?

The visual depiction of data points arranged into user-specified ranges is called a histogram.

Written by Prerit Jain

Content

1. Overview 2. Mean vs Median 3. What is Mean Absolute Deviation (MAD)?4. How to calculate standard deviation 5. How to find z score 6. Percentiles 7. Residuals & Correlation 8. Departure From Linearity 9. Collecting Data 10. Introduction to Probability 11. Introduction to random variables 12. Binomial Random Variables 13. Geometric Distribution - Definition and Solved Examples 14. What is Sampling Distribution?15. What is Normal Distribution?16. Uses and Properties of Density Curves 17. Central Limit Theorem Explained!18. Chi-Square Test

What is Normal Distribution?

What is normal distribution?

The normal distribution is a type of probability distribution that is symmetric about the mean. Data is symmetrically distributed and skew-free in a normal distribution. When the data is shown on a graph, it has the shape of a bell, with the majority of numbers congregating in the center and diminishing as they move outward.

Looking for last minute help for your AP Statistics exam in May? Find an expert 1-on-1 online AP Statistics tutor from Wiingy and give your exam prep a boost!

Normal distribution mathematical formula

The normal probability density formula is:

$\frac{1}{{\sigma \sqrt {2\pi } }}{e^{ - \frac{{{{(x - \mu )}^2}}}{{2{\sigma ^2}}}}}$

$f(x)$ = probability

$x$ = value of the variable

$\mu$ = mean

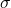$\sigma$ = standard deviation

${\sigma ^2}$ = variance

Properties of normal distribution

The mean, median, and mode have the same values.
Half of the values lie below the mean, and half are above the mean, indicating that the distribution is symmetric about the mean.
The mean and standard deviation are two numbers that may be used to define the distribution.

Normal distributions and the empirical rule

The “68-95-99.7 rule” is another name for the empirical rule, which specifies how data should be dispersed in a normal distribution. According to the rule, approximately:

68% of the data points will be close to the mean in terms of standard deviation.
The mean value and two standard deviations will be shared by 95% of the data points.
Three standard deviations from the mean will be occupied by 99.7% of the data points.

The empirical rule formula is as follows:

Calculate the mean of the values:

$\mu = \frac{{\sum\limits_{}^{} {{x_i}} }}{n}$

Calculate the standard deviation:

$\sigma = \sqrt {\frac{{\sum {{{({x_i} - \mu )}^2}} }}{{n - 1}}}$

Now apply the empirical formula:

Data from 68% of the samples are within one standard deviation of the mean, or between $\mu - \sigma$ and $\mu + \sigma$ .

95% of the data is between 2 standard deviations of the mean, or between $\mu - 2\sigma$ and $\mu + 2\sigma$ .

99.7% of the data lies within 3 standard deviations of the mean, or between $\mu - 3\sigma$ and $\mu + 3\sigma$ .

Qualitative sense of the normal distribution

Some of the important real-life examples of the normal distribution are as follows:

Shoe Sizes: With a mean size of size 10 and a standard deviation of 1, the distribution of shoe sizes for men in the United States is essentially regularly distributed. A bell-shaped pattern with a single peak at size 10 may be seen in a histogram of all male Americans’ shoe sizes.
Retirement age of NFL players: NFL players’ retirement ages are distributed regularly, with a mean age of 33 and a standard variation of around 2 years. This distribution’s histogram displays the traditional bell shape.
IQ: Most parents and kids want to examine the degree of intelligence in an environment of heightened competitiveness. The IQ of a group is represented as a normal distribution curve, with the majority of the population’s IQs falling within the normal range and the remaining individuals’ IQs falling within the deviated range.

The easiest way to identify a normal distribution: The best approach to determine whether a frequency distribution looks to follow a normal distribution is to look at a histogram.

Draw a histogram and study the bar shapes. The distribution is generally regularly distributed if the bars have the shape of a bell or a hill, as in the figure below.

Standard table for proportion below and above

The standard normal distribution table is a collection of regions from the standard normal distribution, sometimes referred to as a bell curve, and it shows the size of the region under the bell curve and to the left of a particular z-score to illustrate probabilities of occurrence in a specific population.

To calculate the z score we use the formula: $\frac{{(x - \mu )}}{\sigma }$

For the below calculations, we use the table to find the proportion and for the above, we get the z-score from the table and we subtract it from 1.

Standard normal distribution

A unique type of normal distribution with a mean of 0 and a standard deviation of 1 is known as the standard normal distribution or z-distribution.

By transforming the values of any normal distribution into z scores, it is possible to standardize it. Z-scores provide the number of standard deviations from the mean that each value falls within.

Conclusion

In this article, we learned what normal distribution is and some of its uses in day-to-day analyses. We learned how to find the mean and standard deviation of the normal distribution and how they are used in the empirical rule. We saw how the standard normal curve can be used to calculate the probability by calculating the z-score of the distribution.

Sample examples

Example 1: The scores of an SAT examination have a normal distribution with a mean of 1000 and a standard deviation of 222. What is the probability a student would score more than 900 on SAT?

Solution 1:

Using the formula, $\frac{{(x - \mu )}}{\sigma }$ we get the z-score to be -0.45

$P(X > 900) = P(Z > - 0.45)$

To find the above value we need to subtract the value from the table from 1.

$1 - 0.3264 = 0.6736$

Therefore, the probability is 0.6736

Example 2: Given that the mean and standard deviation of a normal distribution is 23 and 9 respectively, what is the value in the highest 4% of the distribution?

Solution 2:

$\begin{array}{l}\mu = 23\\\sigma = 9\end{array}$

It is given that the value we need to find needs to be in the top 5%

$\[\]$

$\begin{array}{l} \Rightarrow P(X > y) = 0.04\\ \Rightarrow P(Z > y) = 0.04\\ \Rightarrow P(Z < y) = 1 - 0.5160 = 0.4840 \Rightarrow Z = 0.684\\X = 23 + 0.684(9)\\ = 29.156\end{array}$

Therefore, the value is 29.156

Example 3: The average time students take to solve a problem is 5 minutes with a standard deviation of 2.2 minutes. What is the probability that a student takes between 3 mins and 6 mins to solve the problem?

Solution 3:

Given,

$\begin{array}{l}\mu = 5\\\sigma = 2.2\end{array}$

Now calculating the z-score for 3 mins and 6mins using $\frac{{(x - \mu )}}{\sigma }$ is

$\frac{{(3 - 5)}}{{2.2}} = - 0.91$ and $\frac{{(6 - 5)}}{{2.2}} = 0.45$ respectively.

$\begin{array}{l}P(3 < X < 6) = P( - 0.91 < Z < 0.45)\\ = P(Z < 0.45) - P(Z < - 0.91)\\ = 0.6736 - 0.1841\\ = 0.4895\end{array}$

Therefore, the probability of a student taking between 3 and 6 mins to solve a problem is 0.4895

Example 4: The normal distribution of IQ scores has a mean of 100 and a standard deviation of 18. Use the empirical rule to find the IQs of 68,95 and 99.7 percent of the distribution.

Solution 4:

$\begin{array}{l}\mu = 100\\\sigma = 18\end{array}$

Using the empirical rule formulas.

$\mu - \sigma = 100 - 18 = 82$ and $\mu + \sigma = 100 + 18 = 118$ .

68% of the distribution has an IQ between 82 and 118.

$\mu - 2\sigma = 100 - 36 = 64$ and $\mu + 2\sigma = 100 + 36 = 136$

95% of the distribution has an IQ between 64 and 136

$\mu - 3\sigma = 100 - 54 = 46$ and $\mu + 3\sigma = 100 + 54 = 154$

99.7% of the distribution has an IQ between 46 and 154.

Example 5: A spending distribution has a normal distribution with a mean of $15.65 and a </strong>standard deviation of$ 3.46. What amount corresponds to the 89^th percentile?

Solution 5:

$\begin{array}{l}\mu = 15.65\\\sigma = 3.46\\P(X > y) = 0.89 \Rightarrow P(Z > y) = 0.89\\P(Z < y) = 1 - 0.89 = 0.11 \Rightarrow Z = - 1.227\\X = 15.65 + ( - 1.227)(3.46)\\11.404\end{array}$

Therefore, the amount corresponding to the 89^th percentile is $11.404.

Looking for last minute help for your AP Statistics exam in May? Find an expert 1-on-1 online AP Statistics tutor from Wiingy and give your exam prep a boost!

Frequently asked questions (FAQs)

How many measures of variability are there?

There are four measures of variability which are variance, standard deviation, interquartile range, and range.

What is the t-distribution?

Existing intelligence Compared to the conventional normal distribution; the t-distribution increases the chance of observations in the distribution’s tails.

What are the two types of the probability distribution?

Discrete and continuous probability distributions are the two main categories in which probability distributions fall. There are several varieties of probability distributions within each category. standard deviation.

What is the standard deviation?

A “typical” variation from the mean is shown by the standard deviation. Because it uses the data set’s original units of measurement, it is a well-liked measure of variability.

What is a histogram?

The visual depiction of data points arranged into user-specified ranges is called a histogram.

References

Altman, D. G., & Bland, J. M. (1995). Statistics notes: the normal distribution. Bmj, 310(6975), 298.

Nadarajah, S. (2005). A generalized normal distribution. Journal of Applied statistics, 32(7), 685-694.

Written by

Prerit Jain

See our editorial process Meet our Review board

Previous

Next

Share article on