Binomial Random Variables

Updated on: 08 Dec 2023

Content

1. Overview 2. What is Mean Absolute Deviation (MAD)?3. How to calculate standard deviation 4. How to find z score 5. Percentiles 6. Residuals & Correlation 7. Departure From Linearity 8. Collecting Data 9. Introduction to Probability 10. Introduction to random variables 11. Binomial Random Variables 12. Geometric Distribution - Definition and Solved Examples 13. What is Sampling Distribution?14. What is Normal Distribution?15. Uses and Properties of Density Curves 16. Central Limit Theorem Explained!17. Chi-Square Test

Binomial Random Variables

A binomial distribution is defined as a probability distribution defined on a discrete set of random variables that describes the number of pre-defined successes in an experiment. Since the binomial distribution is defined for a binary experiment, its probability can be described as a binomial expansion where each term represents the probability of a specific number of successes out of n times the experiment is repeated.

Thus, the binomial random variables is defined as the number of successes in an experiment repeated n time. Binomial distributions are the basics in the study of probability distribution which is one of the most important concepts in application-based Statistics.

Looking for last minute help for your AP Statistics exam in May? Find an expert 1-on-1 online AP Statistics tutor from Wiingy and give your exam prep a boost!

What are binomial variables and random variables?

A binomial random variable is a variable that represents the number of successes in an n-times repeated binary experiment (outcomes are either success or failure) and is known as the binomial random variable.

A binomial distribution is described as a probability distribution based on a discrete set of random variables, the symbolic representation of a Binomial distribution, where n represents the number of times the experiment has been repeated, and p is the probability of success in a single iteration of the experiment. A binomial variable is the probability of a random variable in a binomial distribution.

So, the relationship between binomial variables and binomial random variables is that a binomial variable is a specific outcome of a binomial random variable, which is a random variable that follows a binomial distribution

Characteristics of binomial distribution

The binomial distribution is different from other distributions in certain aspects. These are known as the characteristics of binomial distribution or binomial variables and they are given as follows,

Discrete random variable: The random variable for most probability distributions is defined on a continuous interval of the real line, whereas random variables in binomial distributions, also known as binomial random variables, are defined on a discrete subset of the set of non-negative integers since it describes the number of successes, and a number of anything can only be either 0 or a natural number, i.e., non-negative integer.
Exactly two outcomes of the experiment: A binomial distribution can only be defined on a binary experiment, that is, the experiment in a binomial distribution has exactly two outcomes, a success, and a failure. To define a binomial distribution, we divide any non-binary experiment by defining one of the outputs as a success and the rest everything as a failure. But binomial distribution cannot be defined for more than two outcomes.
The number of trials is fixed: The number of trials put the number of repetitions of the experiment. A binomial distribution is fixed, and if we change the number of trials the distribution itself changes completely. While for other distributions defined on continuous random variables, the distribution is independent of the number of trials.
The probability is constant: Since the binomial distribution is defined on a predefined binary experiment thus the probability of success is constant, or we can simply say in a binomial distribution the probability function is independent of the random variable. $P(X) = p,\;\forall \;X < n$ , where X is the random variable and n is the number of trials. While in other distributions, the probability function can be dependent on a random variable based on what the density function is.

Properties of binomial variables

Some distinct properties of binomial distribution distinguish them from other probability distributions. These properties are as follows.

Probability mass function (PMF): The probability mass function is a function defined on the discrete set of random variables in a binomial distribution which describes the weightage of probability around the random variable. In binomial distribution it is described as PMF, whereas in other probability distributions are defined on continuous sets, thus their mass functions are also defined on continuous sets and we call them Probability Density Functions, PDF.
10 percent rule of independence: 10% rule of independence states that, if a sample set of a trial is less than 10% of the total population set, then the trials can be treated as independent.
The expected value of a binomial variable: If we represent the binomial distribution as a statistical probability distribution table (frequency distribution table, with probability replacing the frequency), then if we find the mean value using the formula, $\Sigma XP(X)$ and this mean value is known as the expected value of the binomial random variable.
Variance & standard deviation of binomial variable: Since we can find the mean (expected value), we can also find the variance and standard deviation of the binomial distribution. The variance is given by,

$Var(X) = E({X^2}) - {(E(X))^2}$

And the standard deviation is given by,

$\sigma (X) = \sqrt {Var(X)} = \sqrt {E({X^2}) - (E({X^2}))}$

Applications of binomial distribution

Binomial Distribution is very useful in many real-life practices, we find the applications of binomial distribution in various situations and mathematical problems some of the applications are given below,

Statistical inference
Quality control
Forecasting
Data analysis

Identifying a binomial distribution

Binomial distribution has many different terms and identifiers which can be used to determine if a given distribution is a binomial distribution or not and to calculate probabilities for different random variables.

Identifying the fixed number of trials: A binomial variable is defined on a finite discrete set of random variables, thus the maximum of this set is also known as the number of trials since random variables represent the number of successes and the maximum number of successes can only be equal to the number of trials and it must be finite.
Identifying the two outcomes: A binomial distribution is defined for a binary experiment, i.e., there are only two possible outcomes, a success or a failure. Thus, we need to check if for the given distribution we have exactly only two possible outcomes.
Identifying the constant probability of success: In a binomial distribution, the probability of success (or failure) in an individual round of the experiment is independent of the number of rounds, i.e., the probability of success (or failure) is constant.

Conclusion

In this article, we have learned about binomial distributions and binomial random variables. A binomial distribution is a probability distribution defined on a finite discrete set of random variables, for a fixed number of trials of a binary experiment, i.e., there are only 2 possible outcomes to one trial of the experiment, either success or failure.

A binomial variable function is the probability of a random variable in a binomial distribution. When represented as a probability distribution table, binomial distribution can be used to calculate expected value, variance, and standard deviation random variable.

Solved examples

Now let’s see some questions based on Binomial Probability distributions.

Example 1: Find the probability of 5 heads in 7 tosses of a coin.

Solution: Here in this question, we have 7 total coin tosses, so the number of trials is a fixed finite number, i.e., 7.

Also, a coin toss has only two outcomes and we are given that we need to find the probability of heads, so we can consider getting a head on a toss as our success, then we have

$p = P(Success) = \frac{1}{2}$

And then, the probability of failure would be,

$q = \frac{1}{2}$

Hence, the probability of success and failure is a constant independent of the number of trials or random variable, thus the given question can be represented by the following Binomial Variable,

$Binomial\_Variable(7,\frac{1}{2})$

To calculate,

$P(5) = \left( {\begin{array}{*{20}{c}}7\\5\end{array}} \right){\left( p \right)^5}{\left( q \right)^{7 - 5}}$

In this calculation, the term

$\left( {\begin{array}{*{20}{c}}7\\5\end{array}} \right)$

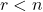is called a binomial coefficient and it is pronounced as 7 choose 5, and the formula for any n choose r, $r < n$ , is given by

$\left( {\begin{array}{*{20}{c}}n\\r\end{array}} \right) = \frac{{n!}}{{r!(n - r)!}}$

Then we have,

$\begin{array}{l}P(5) = \left( {\begin{array}{*{20}{c}}7\\5\end{array}} \right){\left( {\frac{1}{2}} \right)^5}{\left( {\frac{1}{2}} \right)^2}\\P(5) = \left( {\begin{array}{*{20}{c}}7\\5\end{array}} \right){\left( {\frac{1}{2}} \right)^7}\\P(5) = \frac{{7!}}{{5!(7 - 5)!}} \times \frac{1}{{128}}\\P(5) = \frac{{7 \times 6}}{{2 \times 1}} \times \frac{1}{{128}}\\P(5) = \frac{{21}}{{128}}\end{array}$

Hence, the probability of getting 5 Heads in 7 coin tosses is 21 out of 128.

Example 2: Find the Expected value and Standard Deviation, in a binomial distribution, when the total number of trials is given to be 5 and the probability of success is $\frac{1}{2}$ .

Solution: Let’s make a Probability distribution table from the given Binomial Distribution

$X$	$P(X)$	$XP(X)$	${X^2}$	${X^2}P(X)$
0	$^5{C_0}{\left( {\frac{1}{2}} \right)^0}{\left( {\frac{1}{2}} \right)^5} = \frac{1}{{32}}$	0	0	0
1	$^5{C_1}{\left( {\frac{1}{2}} \right)^1}{\left( {\frac{1}{2}} \right)^4} = \frac{5}{{32}}$	$\frac{5}{{32}}$	1	$\frac{5}{{32}}$
2	$^5{C_2}{\left( {\frac{1}{2}} \right)^2}{\left( {\frac{1}{2}} \right)^3} = \frac{{10}}{{32}}$	$\frac{5}{8}$	4	$\frac{5}{4}$
3	$^5{C_3}{\left( {\frac{1}{2}} \right)^3}{\left( {\frac{1}{2}} \right)^2} = \frac{{10}}{{32}}$	$\frac{{15}}{{16}}$	9	$\frac{{45}}{{16}}$
4	$^5{C_4}{\left( {\frac{1}{2}} \right)^4}{\left( {\frac{1}{2}} \right)^1} = \frac{5}{{32}}$	$\frac{5}{8}$	16	$\frac{5}{2}$
5	$^5{C_5}{\left( {\frac{1}{2}} \right)^5}{\left( {\frac{1}{2}} \right)^0} = \frac{1}{{32}}$	$\frac{5}{{32}}$	25	$\frac{{25}}{{32}}$
		$\Sigma XP(X) = \frac{{15}}{8}$		$\Sigma {X^2}P(X) = \frac{{210}}{{32}}$

The mean/Expected value is given by,

$\begin{array}{l}E(X) = \Sigma XP(X)\\E(X) = \frac{{15}}{8}\\E(X) = 1.875\end{array}$

Variance is given by,

$\begin{array}{l}Var(X) = E({X^2}) + {(E(X))^2}\\Var(X) = \frac{{210}}{{32}} + {\left( {\frac{{15}}{8}} \right)^2}\\Var(X) = \frac{{210}}{{32}} + \frac{{225}}{{64}}\\Var(X) = \frac{{420 + 225}}{{64}}\\Var(X) = \frac{{625}}{{64}}\end{array}$

And the standard deviation,

$\begin{array}{l}\sigma (X) = \sqrt {Var(X)} \\\sigma (X) = \sqrt {\frac{{625}}{{64}}} \\\sigma (X) = \frac{{25}}{8}\\\sigma (X) = 3.125\end{array}$

Hence the Expected value is 1.875 and the variance is 3.125.

Example 3: Find the probability of getting a composite number at least three times on 4 throws of an unbiased dice.

Solution: Here we have, 4 throws of an unbiased dice, i.e., the number of trials is a fixed finite number. Next, we need to calculate the probability of getting a composite number, so we can define success in a trial as getting a composite number. Hence, we have

$p = P(Success) = \frac{2}{6} = \frac{1}{3}$ (We have 2 composite numbers, 4 and 6, out of 6 total outcomes)

And the corresponding failure is,

$q = 1 - p = 1 - \frac{1}{3} = \frac{2}{3}$

Since we need to find the probability of at least 3 composite numbers, then we have the random variable, $X \ge 3$ .

$P(X \ge 3) = P(X = 3) + P(X = 4)$

Then calculate the probability of 3 composite numbers,

$\begin{array}{l}P(3) = {\;^4}{C_3}{p^3}{q^{4 - 3}}\\P(3) = \frac{{4!}}{{3!1!}}{\left( {\frac{1}{3}} \right)^3}{\left( {\frac{2}{3}} \right)^1}\\P(3) = 4 \times \frac{2}{{81}}\\P(3) = \frac{8}{{81}}\end{array}$

And the probability of 4 composite numbers,

$\begin{array}{l}P(4) = {\;^4}{C_4}{p^4}{q^{4 - 4}}\\P(4) = \frac{{4!}}{{4!0!}}{\left( {\frac{1}{3}} \right)^4}\\P(4) = 1 \times \frac{1}{{81}}\\P(4) = \frac{1}{{81}}\end{array}$

And finally,

$\begin{array}{l}P(X \ge 3) = P(3) + P(4)\\P(X \ge 3) = \frac{8}{{81}} + \frac{1}{{81}}\\P(X \ge 3) = \frac{9}{{81}}\\P(X \ge 3) = \frac{1}{9}\end{array}$

Thus, the probability of at least 3 composite numbers in 4 throws of unbiased dice is 1 out of 9.

Looking for last minute help for your AP Statistics exam in May? Find an expert 1-on-1 online AP Statistics tutor from Wiingy and give your exam prep a boost!

Frequently asked questions (FAQs)

References

Altham, P. M. (1978). Two generalizations of the binomial distribution. Journal of the Royal Statistical Society: Series C (Applied Statistics), 27(2), 162-167.

Edwards, A. W. F. (1960). The meaning of binomial distribution. Nature, 186(4730), 1074-1074.

Written by

Prerit Jain

See our editorial process Meet our Review board

Share article on