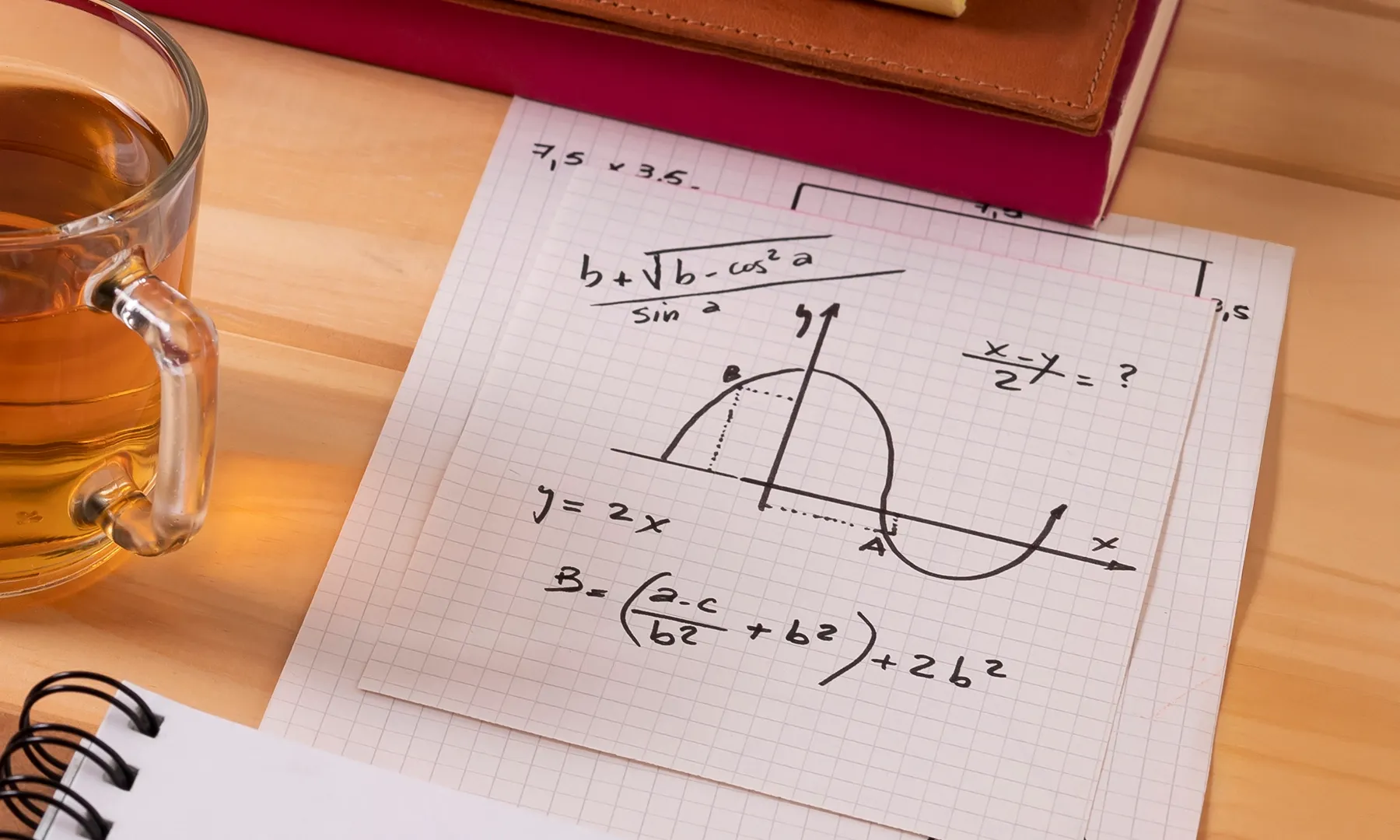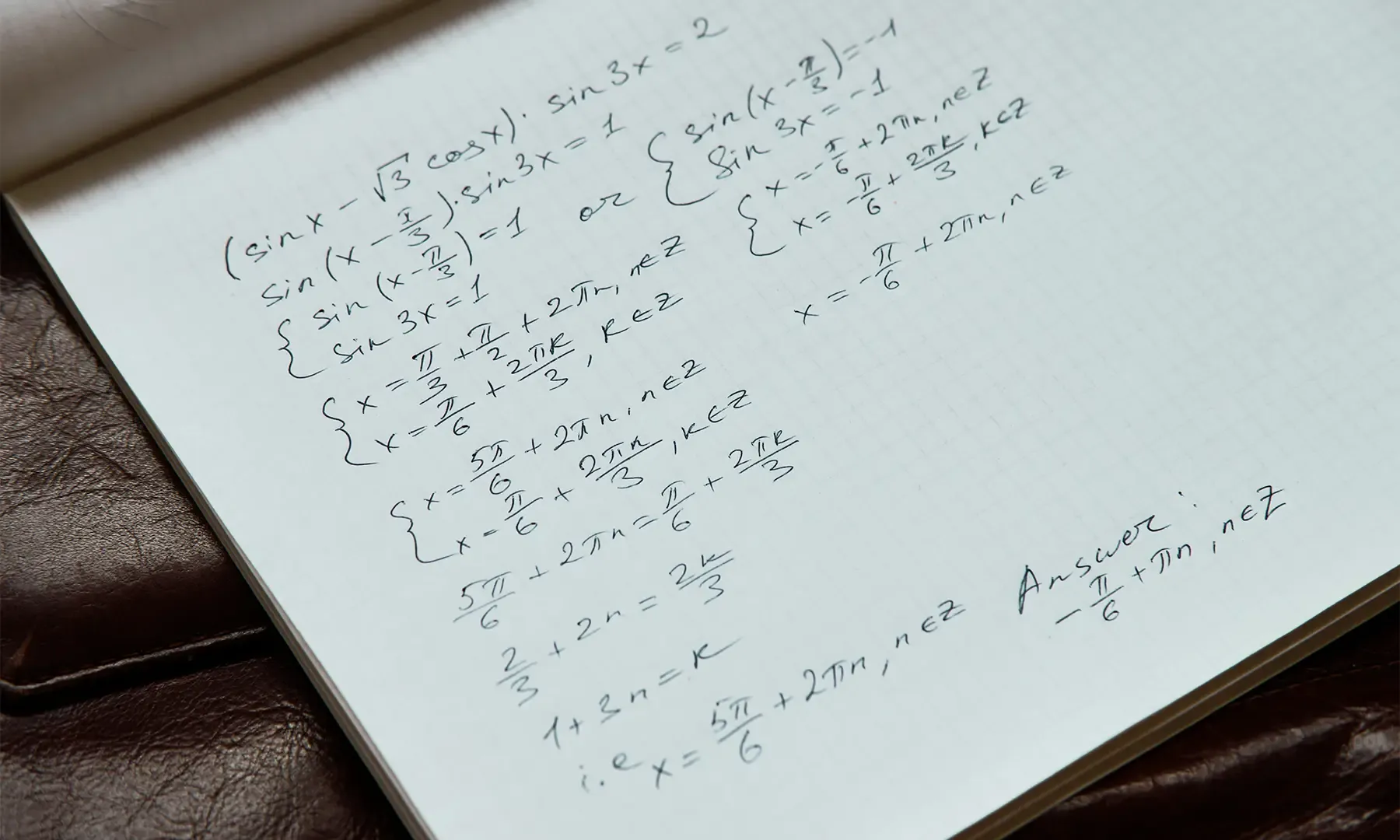Calculus tutor near me in Australia
Succeed through personalised help from calculus tutors
Calculus tutors for school and uni students

Recent Calculus classes in AU
Calculus classes are delivered in Sydney, Perth, Hobart
Taruna taught 3 months ago
The session focused on calculus problems, including implicit differentiation, trigonometric substitution, domain determination, integration techniques (u-substitution, partial fractions), surface area calculations, and solving differential equations. The Student practiced applying formulas and methods for each topic. The next session will be on Wednesday at 2 p.m. to review another practice test.
Implicit Differentiation
Simplification Using Trigonometric Substitution
Domain Restrictions and Trigonometric Functions
Integration Using Substitution and Trigonometric Identities
Partial Fraction Decomposition
Surface Area of Revolution
Exact Differential Equations
Taruna taught 4 months ago
An instructor and a learner from Phoenix worked through several calculus problems, including partial fraction decomposition, trigonometric substitution, finding partial derivatives, sketching domains, applying the washer method, and solving differential equations. The learner practiced identifying appropriate methods for solving each problem type. The instructor assigned them to practice exact differential equations for the next lesson.
Integration by Substitution (Definite)
Integration by Parts (for ln)
Linear Differential Equations
Washer Method for Volume
Domain of a Root Function
Partial Fractions Integration
Taruna taught 4 months ago
Taruna and Greta delved into differential equations during their recent calculus lesson, specifically reviewing separable, linear, and exact types. They worked through several problems for each, with Greta focusing on identifying the correct method and applying various integration techniques. Greta will now practice additional problems and can ask questions during their next lesson or before her test next week.
Separable Differential Equations
Linear Differential Equations
Exact Differential Equations
Partial Fractions in Integration
Taruna taught 4 months ago
Taruna and Greta continued their calculus studies, with Taruna assisting Greta in a recent lesson focused on multi-variable functions. They delved into partial derivatives, domain and range calculations, and the application of the chain rule. Greta practiced numerous problems involving logarithmic, exponential, and trigonometric functions, specifically working through finding partial derivatives and using the chain rule in multi-variable contexts. Their emphasis was on understanding the foundational formulas and effective substitution methods.
Partial Derivatives
Domain of Multivariable Functions
Range of Multivariable Functions
Multivariable Chain Rule
Mixed Partial Derivatives
Taruna taught 4 months ago
In a recent calculus lesson, Taruna guided Greta through volume calculations, employing both the disk/washer and cylindrical shell methods. Their work emphasized sketching regions and accurately setting up integrals. Additionally, they tackled finding arc lengths of various curves. They've scheduled their next lesson to continue with workshop 8.
Volume of Revolution (Disk/Washer Method)
Revolving About a Line (y=c or x=c)
Cylindrical Shell Method
Arc Length Formula
Taruna taught 5 months ago
During a calculus lesson, a learner, a student at Chaffey College in Rancho Cucamonga, worked through various problems. The lesson focused on derivatives, integrals, and domain calculations. The student practiced finding intercepts, intervals of increasing/decreasing functions, local extrema, u-substitution, and integration by parts. They also spent time determining domains. The instructor recommended further practice with integrals to solidify understanding of the methods discussed.
X-Intercepts of Cubic Functions
First Derivative Test
Second Derivative Test
Integration by Partial Fractions
Domain of Multivariable Functions
Variable Separable Differential Equations
Linear Differential Equations
Learning calculus in Australia: 7 common questions answered
When do students first study calculus in Australia?
Students are introduced to calculus in senior secondary school, typically in Year 11 or 12. In New South Wales, calculus appears in HSC Mathematics Advanced and Extension courses. In Victoria, it’s covered in VCE Mathematical Methods and Specialist Mathematics. Queensland students explore it through ATAR Maths Methods and Specialist. These courses form the foundation for university-level study in fields like engineering, science, commerce, and health.
Why is calculus often seen as one of the hardest maths topics?
Calculus brings together many skills at once including algebra, functions, graphs, and real-world modelling. Students are expected to understand the concept of a limit, compute derivatives, interpret rates of change, and work with areas under curves. What makes it hard is that small mistakes can derail entire problems, and many questions involve multiple steps of reasoning.
How is calculus assessed in senior school?
Calculus is assessed through written exams that require explanation, reasoning, and accurate working. VCE and HSC exams include both straightforward problems and applied scenarios using calculus concepts. Questions may ask students to sketch functions, analyse motion, or solve real-world optimisation problems. Internal school assessments throughout the year also contribute to final ATAR results.
What careers or uni degrees require calculus?
Calculus is essential for degrees in engineering, physics, data science, actuarial studies, computer science, and health sciences. Universities like the University of Melbourne, UNSW, UQ, and ANU include calculus-based units in first-year programs. Students entering commerce, economics, or even architecture may also encounter calculus in quantitative subjects.
What are some useful resources to learn or revise calculus?
Australian students often use Edrolo, Jacaranda Maths Quest, or Cambridge textbooks aligned to their curriculum. Visual tools like Desmos, GeoGebra, and Khan Academy help with graphing and conceptual understanding. Past exam papers from VCAA, NESA, or QCAA are also excellent for timed practice and identifying common problem types.
How can students build confidence with calculus?
Confidence builds through consistent practice, not cramming. Breaking down each topic like limits, derivatives, and integrals into smaller steps helps. Students should regularly solve problems, revisit errors, and use feedback from teachers. Studying in pairs or small groups can also make revision more engaging and less isolating.